Como afecta el algoritmo al rendimiento (o resolviendo una pregunta de Google)
Sunday, April 11th, 2010Tras nueve meses de sequía bloguera, vuelvo con un post bastante parecido al de “Exponenciación modular” (uno de los que más visitas tiene) que toca uno de los temas que me apasionan: el rendimiento de los algoritmos. Hace bastantes meses leí, via meneame, un post con 140 preguntas que (supuestamente) Google puede hacerte en una entrevista de trabajo. Una de esas preguntas me llamó la atención, tanto que unos cuantos compañeros del trabajo la estuvimos comentando. Te pedían que escribieras un algoritmo muy simple:
Dado un array A[N] de N números. Tienes que generar un array Ouput[N] de manera que Output[i] sea la multiplicación de todos los elementos de A[N] excepto A[i]. Por ejemplo Output[0] será la multiplicación desde A[1] hasta A[N-1] y Output[1] sera la multiplicación de A[0] y desde A[2] hasta A[N-1]…
En ruby es tan sencillo como:
n = A.length Ouput = Array.new(n) do |i| result = 1 n.times { |j| result *= A[j] unless j == i } result end |
El problema es que la pregunta continuaba con:
… hazlo en O(n) …
Ups, hay que repensarlo ya que el algoritmo anterior tiene dos bucles sobre N anidados por lo que es O(n2). Se me ocurrió hacerlo precalculando el producto de todos los elementos de A[N] y hacer que Output[i] = Total / A[i]. Así queda O(n).
product = A.inject(1) { |total, n| total * n } Output = A.collect { |n| product / n } |
Pero faltaba un último detalle de la pregunta:
… sin el operador de división.
Uff, ahora se pone interesante. Tras pensarlo un poco y escribir Ouput como una matriz de los elementos a multiplicar, ví un patrón que me podía servir. La matriz está formada por dos “triángulos” (perdón si el termino no es correcto. Hay algún matemático entre la audiencia?) que llamaremos L, resaltado en azul, y R, en rojo.
Output[0] = [ 1, A[1], A[2], ..., A[N-1]] Output[1] = [A[0], 1, A[2], ..., A[N-1]] Output[2] = [A[0], A[1], 1, ..., A[N-1]] ... Output[N-1] = [A[0], A[1], A[2], ..., 1]
Se me ocurrió que esos dos “triángulos” o productos parciales se podían calcular a la vez en un único bucle para usarlos posteriormente para calcular Ouput[i] = L[i] * R[i] ya que:
- L[i] = L[i-1] * A[i-1] para i > 0 (L[0] = 1)
- R[i] = R[i+1] * A[i+1] para i < N-1 (R[N-1] = 1)
n = A.length left,right = Array.new(n, 1), Array.new(n, 1) 1.upto(n-1) do |i| left[i] = left[i-1] * A[i-1] right[n-(i+1)] = right[n-i] * A[n-i] end Output = Array.new(n) { |i| left[i] * right[i] } |
Bien, creo que al final lo hemos conseguido. Un algoritmo O(n) que no usa la división y que calcula los resultados según la formula indicada. Además, el algoritmo que usa la división tiene un problema: necesita que los elementos de A[N] sean números naturales (es decir, que no puedan ser 0) mientras que los otros dos algoritmos no tienen esta restricción.
Si os estáis preguntando si realmente hay diferencia de rendimiento entre los tres algoritmos (principalmente el primero versus los otros dos), aquí tenéis un gráfico que lo demuestra.
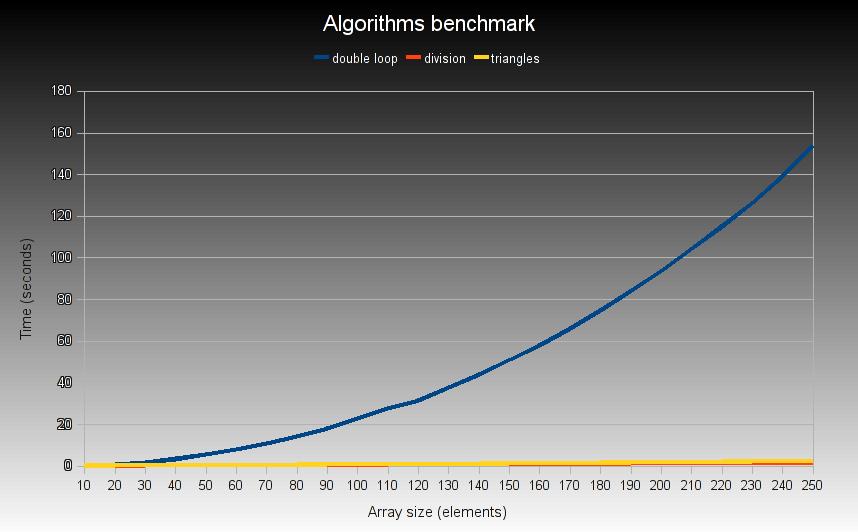
Como se puede ver, a medida que el tamaño del array A[N] crece los tiempos del primer algoritmo (double loop) crecen exponencialmente mientras que los otros dos (division y triangles) tienen un comportamiento lineal. Por tanto, si que hay diferencia, y mucha.
Los datos de benchmarking para generar el gráfico con el OpenOffice.org Calc los he obtenido he usado el siguiente script que genera CSV.
#! /usr/bin/env ruby require 'benchmark' def double_loop(input) n = input.length Array.new(n) do |i| result = 1 n.times { |j| result *= input[j] unless j == i } result end end def division(input) product = input.inject(1) { |total, n| total * n } input.collect { |n| product / n } end def triangles(input) n = input.length left,right = Array.new(n, 1), Array.new(n, 1) 1.upto(n-1) do |i| left[i] = left[i-1] * input[i-1] right[n-(i+1)] = right[n-i] * input[n-i] end Array.new(n) { |i| left[i] * right[i] } end t = 1_000 max_size = 250 step_size = 10 step_size.step(max_size, step_size) do |n| input = Array.new(n) { rand(100) + 1 } t1 = Benchmark.realtime { t.times { double_loop(input) } } t2 = Benchmark.realtime { t.times { division(input) } } t3 = Benchmark.realtime { t.times { triangles(input) } } puts "#{input.length};#{t1};#{t2};#{t3}" end |
Por cierto, si a alguién se le ocurre otro algoritmo que lo ponga en los comentarios.