El otro día, no recuerdo muy bien a cuento de qué, me acordé de la exponenciación binaria, que es un algoritmo de exponenciación en aritmética modular que me explicó un profesor en el año que cursé Ingeniería de Telecomunicaciones en la UPC. Desde entonces siempre había tenido curiosidad por averiguar cual sería la diferencia en cuanto a tiempo de cálculo entre hacer la exponenciación por el método clásico o hacerla usando el algoritmo que me explicaron. Cansado de tener esta duda rondando por mi mente decidí hacer algo al respecto en un rato que tenía más o menos libre y aquí expongo mis resultados. ATENCIóN: Estos resultados son muy aproximados así que no los toméis muy en serio, sólo como orientación.

No voy a entrar en explicar que es la aritmética modular, para ello ya tenemos una página en la wikipedia, incluso hay una página dedicada a la exponenciación modular.

El método clásico se resume en ir multiplicando la base por ella misma tantas veces como indique el exponente (que es la definición de exponenciación), pero tras cada multiplicación hay que calcular el módulo del resultado para que el resultado temporal no crezca excesivamente:

t=base;
for (i=0; i<exp; i++) {
    t = (t * base) % modulo;
}
resultado = t;


Usando este algoritmo, debemos realizar tantas multiplicaciones y operaciones de módulo como indique el exponente. Es decir, si el exponente es 1000, necesitaremos 1000 multiplicaciones y 1000 divisiones (el cálculo del módulo es una división de la cual nos quedamos con el resto en lugar de con el resultado de la división).

El algoritmo de exponenciación binaria es más complejo pero permite realizar el cálculo con un menor número de operaciones. Se basa en descomponer el exponente en suma de potencias de 2. Inicializamos la variable temporal con el valor de la base. Empezando por el segundo bit más significativo del exponente mientras no lleguemos al bit menos significativo hacemos lo siguiente: multiplicamos la variable temporal por ella misma (lo elevamos al cuadrado), si el bit actual es igual a 1 multiplicamos la variable temporal por la base, y finalmente calculamos el módulo:


t=base;
for (i=numero_bits(exponente)-1; i>0; i--) {
    t = (t * t);
    if (bit(i, exponente) == 1)
        t = t * base;
    t = t % modulo;
}
resultado = t;


Con este algoritmo, el número de multiplicaciones depende del número de bits y del peso de Hamming(número de 1s) del exponente. Poniéndonos en el peor de los casos, que sería que todos los bits del exponente fueran 1, necesitaríamos tantas multiplicaciones como dos veces el número de bits del exponente. En cuanto al número de divisiones, depende sólo del número de bits.

Para simplificar, consideraremos que el coste computacional de la operación de multiplicar es el mismo que el de calcular el módulo. Entonces, si e es el exponente, con el algoritmo hemos pasado de necesitar 2e operaciones a, como máximo, necesitar 3log₂(e). Es decir, el número de operaciones pasa de crecer linealmente con el exponente a hacerlo de forma logaritmica. Por ejemplo, si el exponente fuera 1023, pasaríamos de utilizar 2046 operaciones a 30.

Vale, sabemos que hay mucha diferencia en el número de operaciones, pero todavía no hemos visto como afecta esto al tiempo de ejecución. Como tampoco tenía mucho tiempo para dedicarle, decidí hacer dos bash scripts:

• Exponenciación clásica
• Exponenciación binaria

Una primera ejecución ya pone de manifiesto la gran diferencia que hay entre los dos algoritmos:

daneel@trantor:~$ export TIMEFORMAT="Tiempo: %Rs"
daneel@trantor:~$ time ./modexp1.sh 7 513 133
77
Tiempo: 2.280s
daneel@trantor:~$ time ./modexp2.sh 7 513 133
77
Tiempo: 0.207s


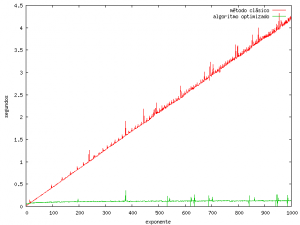
Los dos scripts calculan 7⁵¹³ mod 133, pero uno necesita 2.28 segundos mientras que el otro sólo 0.20. Para tener una comparativa más amplia, he ejecutado los dos scripts cambiando el exponente entre 1 y 1024, y recogiendo el tiempo que ha tardado el script en calcular el resultado. Después, con gnuplot he hecho la gráfica:

Creo que sobran las palabras. La diferencia es asombrosa. Así y todo, el algoritmo aquí comentado no es el más rápido, en el libro “Applied Cryptography” de Bruce Schneier hay un capitulo dedicado a la aritmética modular y explican uno todavía más rápido pero más complejo.

Igual os preguntáis para que sirve esto, pues por ejemplo en el sistema de criptografía de clave asimétrica RSA se realizan operaciones de exponenciación en aritmética modular a la hora de cifrar o descifrar el mensaje. O sea que dependiendo del algoritmo de exponenciación utilizado, tardaremos más o menos en cifrar/descifrar el mensaje.

Por cierto, en la wikipedia también explican la exponenciación binaria usando un algoritmo recursivo.

Bueno, yo ya me he quitado la curiosidad y espero haberos entretenido un ratillo

Informática